数学是人类的高级思维活动，越往顶层走，需要的各种思维能力就越多。所以，要想孩子数学好，首先要帮他“打牢思维的地基”。

怎么打？观看数学纪录片绝对是个不错的选择，无论作为兴趣启蒙，还是培养数学思维，今天要提及的10部顶级数学纪录片绝对值得观看和收藏！

这10部必看的数学纪录片是

数学的故事（The Story Of Maths）

如何提高孩子学习数学的兴趣？不如先从故事的角度了解数学的进化史，感受一下数学大咖们是如何接触那些世纪难题的。

这部《数学的故事》是BBC的4集科学史纪录片，在分析科学进步内在动因的同时，史诗般地还原了数学科学迤逦前行的整个进程，通过在对“东方数学”体悟和对“西方数学”构建的冲突和融合中，百科全书式直视科学思想史全景，再现文明瑰丽绽放的经典时刻。

主讲人Marcus du Sautoy 是一位数学教授，他带领观众走访数学家的故乡，来到这些经典时刻发生之地，真实地呈现牛顿、莱布尼兹、高斯等数学家探索著名理论的历程。

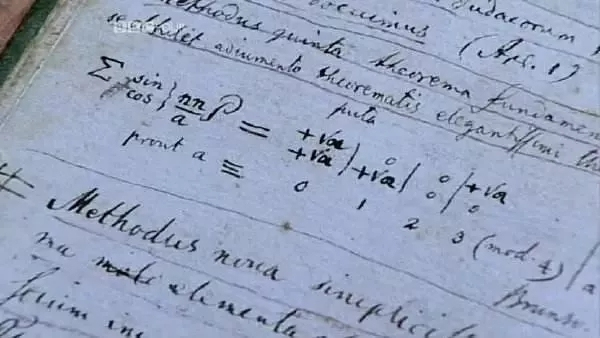
纪录片前两集讲述数学的起源，展现文明古国的先辈们在生产生活中的发明和创造。其中，中国的贡献主要是中国剩余定理和秦九韶用类似牛顿的方法求高次方程的近似解。第三集主要介绍自希腊帝国灭亡后、工业革命之前的数学世界。第四集讲述最近300年的演变历史。

这场意义不凡的旅行，展现了数学这门科学波澜壮阔的历史场景。由古及今，在探索数学的征途中，我们一直都在路上。

统计学的乐趣（The Joy of Stats）

看到“统计学”，你首先想到什么？是让人眼花缭乱的表格，还是各种晦涩难懂的术语？掌握分析数据的能力，能让我们跳出直觉理性严谨思考问题。

在BBC的这部纪录片中，明星教授Hans Rosling用新奇的方式、先进的技术和幽默的语言，讲述了很多奇奇怪怪的统计案例。

他用统计学结合电脑科技展现了一幅我们从未见过的画面，也是我们从来无法想象到的画面。比如，平均数是统计中一个很重要的概念，但是光看它，却会得出一个荒谬结论：把马云和6个穷人放在一起，平均每个人都坐拥好几个亿的财富。

再比如，把来自不同地方的香蕉放在猩猩和大学生面前，猩猩能选出来，大学生却只能瞎猜。如果猩猩选择的正确率更高，能说明动物比人类聪明吗？

这些例子让我们看到，统计学并非简单地处理数字，而是用相关性揭示一些人们忽略的原理。

终极密码（The Code）

揭开事物背后的数字规律，我们生活在一个充满数字的抽象世界！

我们一直在探寻人类最古老的一个疑问：为什么世界是这个样子的？从宏伟的大教堂到北美的周期蝉，从多佛比目鱼到蜿蜒的海岸线，从海洋深处的鹦鹉螺，到美妙的音乐，从繁忙的机场，到浩瀚的星空……正是它们一起构成了密码世界—— 一个充满了数字的抽象世界。

数学规律、几何定律，影响了生物的繁衍，影响了星体的运行，支撑着教堂的穹顶。这是一个神奇而迷人的世界，它与我们真实生活的世界大不相同。

这部同样来自BBC的纪录片共有3集，分别从“数字、形状、预测”三个方向探寻隐藏在宗教、建筑、艺术、生物等大自然和人类生活中的终极密码——数学。

数字间有着令人迷惑的奇妙的联系，只有通过这些密码我们才能了解掌控着整个宇宙的法则，从而揭开这个世界的真相。

生命的历程是求真、求善、求美的过程。数学为什么吸引我们？因为她就是真善美的化身，是生命真谛的呈现。本片用震撼的视觉语言，从点滴的生命现象阐释了数学的真善美。

伟大的疯狂（A Brilliant Madness）

在无常命运中保持美丽心灵的数学家约翰·纳什。

比起艺术化的电影《美丽心灵》，这部纪录片更值得一看，因为它更完整地记录了纳什的生平，并且对理论发现的全过程进行了更深入的探索。

纳什在事业一帆风顺时罹患精神分裂症，面对只能好转、无法治愈的疾病，他在妻子的陪伴下不懈努力，完全通过意志力工作，最终战胜心魔，并登上科研的巅峰。他的一生，在得与失的博弈中取得了均衡。

1950年，22岁的纳什博士毕业，仅仅27页的博士论文中提出了一个重要概念，也就是后来被称为“纳什均衡”的博弈理论。在纳什看来，数学能揭示命运的规律、人生的奥秘。这就是为什么他不满足于像其他数学学者一样，用现有的理论解决问题、发表论文。

在上世纪70年代，纳什的博弈论被运用到了美国的经济建设和国际贸易等实际领域，产生了巨大的影响力。1994年，他和其他两位博弈论学家共同获得了诺贝尔经济学奖。

纪录片告诉我们：要去欣赏一个人在某些方面的天赋，即使他有些古怪，看问题的角度与众不同，那些人通常都是有真正非凡的洞察力。

数学大谜思（The Great Math Mystery）

数学散步在大自然的各个角落，大自然比人类更懂它！

把几朵花放在一起，你可能会从中读出13世纪希腊数学家发现的斐波那契数列：1，2，3，5，8，13……即相邻的两个数相加，总能得到下一个数。这个数列时常出现在大自然中，比如向日葵的种子、松果的底部。

更让人惊讶的是，动物的数学能力远超人类的想象。比如，马达加斯加的狐猴就特别聪明，在没有任何标示的情况下，它们可以自己选出数值更多的食物。

数学，散布在大自然的各个角落中，很多迷思甚至至今都无法解释。这部纪录片从这些极富趣味的细节切入，向观众展现最有趣的数学！

逻辑的乐趣（The Joy of Logic）

逻辑是哲学、语言、数学的引擎！

本片中，一位萌哒哒的教授以轻松有趣深入浅出的方式，讲述逻辑的发展史，什么是逻辑？合乎逻辑意味着什么？逻辑的乐趣是什么？

一根绳子有多长？（How Long Is a Piece of String?）

测量地越精细，绳子就越长！

英国著名演员艾伦·戴维斯试图回答，发现这个问题很快就变成了一个令人费解的古怪难题。艾伦拜访了数学界领军人物马科斯·杜·索托伊，他惊人地发现自己手中这根有限长度的绳子，在原子标度下，居然是无限长。

艾伦甚至还发现，至少在理论层面上，这根短小的绳子将很可能创建一个将世界陷入末日的黑洞。一厘米将有一个新的含义，你是否会开始质疑现实生活中的构造？你测量地越精细，绳子就越长！

纪录片还展现了不少有趣的知识，比如早期的埃及人喜欢用手肘到中指的长度作为标准等等。

在这里，特别推荐一下BBC Horizon地平线系列纪录片，这一系列始于1964年，涵盖了历史、人文、宗教、地理、设计、艺术、生物、哲学、环保、伦理等多个领域的知识，非常适合给孩子做科普启蒙。

寻找隐藏的维度（Hunting the Hidden Dimension）

电影特效也得依靠数学理论！

纪录片告诉我们：这些看似八竿子打不着的东西之所以能联结在一起，全靠数学家本华·曼德博，他发现了“分形”理论，彻底改变了人们的思维。

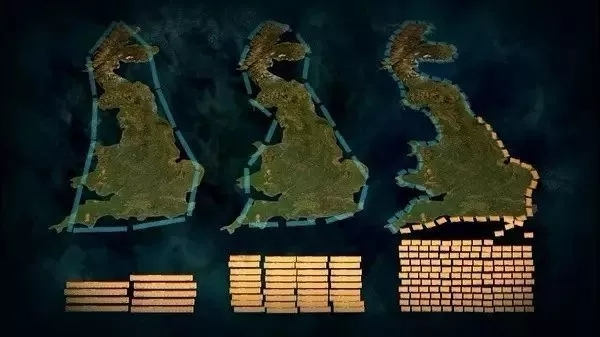
“分行”是本华·曼德博自己创造的一个词，用于描述那些看上去参差又残缺的图形。这一理论问世后，解决了绘制和设计方面的很多难题，好莱坞科幻电影《星际迷航》就是运用“分行”理论才做出了精彩绝伦的特效。

维度：数学漫步（Dimensions:A Walk Through Mathematics）

帮小科幻迷搞懂“四维空间”！

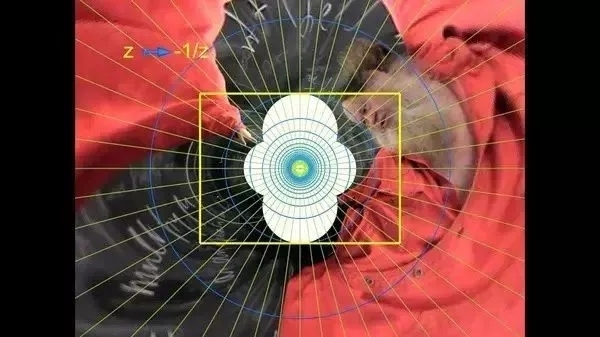
数学家Hipparchus介绍了两数如何描述球面上之点。他接着解释了球极投影法：我们要如何在一张纸上描绘出地球呢？

数学家 Ludwig Schl?fli 介绍了存在于四维空间中的物体，让我们见识到了一系列奇形怪状的四维正多面体。它们有着24、120、甚至600个面！数学家Adrien Douady讲解复数， 以简单的术语解释负数的平方根，变换平面，图片形变， 创造分形图形等知识。

或许不明觉厉，但这些脑洞大开的理论仍然可以让人感受到数学的奇妙！

神秘的混沌理论（The Secret Life of Chaos）

看过本片后，孩子眼中的世界会变得与众不同！

在本部纪录片中，吉姆·奥卡利里教授带着宇宙是如何由从尘埃中诞生，又是如何孕育出智慧生命的难题，开始了他的探秘旅程，探索神秘的混沌理论，试图揭开这层归因于神奇或者上帝力量的神秘面纱。

混沌中的数学可以解释宇宙中从无序中产生有序的神奇景象，他揭示出大自然那些令人叹为观止的美丽和结构中隐藏的科学规律，它是物理定律的固有的组成。看过本片之后，孩子眼中的世界会变得与众不同！

编辑：金婉霞
责任编辑：姜澎

来源：微信公众号“极客与数学”