
证明黎曼猜想的,将是中国人?
10月13日,82岁北京大学退休数学教授李忠,在中科院以内部讨论组的形式做了关于证明黎曼猜想的报告。此次报告长达2小时,得到了北京大学数学学院院长、副院长等专家十分中肯的评价,称“黎曼猜想已被证明”。最终的论文评估结果,相信将在不久也会对外公布。
黎曼猜想被中国人证明了?!
上周六,名为“数学文化”(微博认证为:数学文化主编、南方科技大学数学教授汤涛院士)的微博发布消息:据说李忠教授已经在中科院数学所南楼做了用Reich定理证明黎曼猜想的报告,希望结果正确!
对于李忠教授报告的具体时间,现在有两种说法:一为10月12日,另一个说是10月13日14:30-16:30,李忠教授在中科院以内部讨论组的形式做了关于证明黎曼猜想的报告。


但不管如何,报告会的内容显然比时间重要!在当天题为“黎曼猜想的证明——从 Atiyah 的证明讲起”的报告中,李忠教授给出了一个和此前英国“数学教父” Atiyah 爵士思路不同但含有更多推导过程的证明。
据悉,此次李忠对黎曼猜想的证明并不是直接的。他提出了一个与黎曼猜想等价的猜想,并对这一猜想进行证明。此次证明主要从他自己的一项创新:Reich 度量出发,通过这种新的度量,黎曼猜想可以用纯数学的方式进行证明,而不需要像之前海德堡论坛上 Atiyah 爵士那样借用物理学常数。
此前,Atiyah 爵士在海德堡论坛上宣称的证明方法,则更多只是提出一个大致思路,缺乏细节。Atiyah 爵士证明灵感主要来源于其在 2018 年国际数学家大会上提出的精细结构常数的推演,同时应用了其导师一手开创的 Todd 函数参与计算。虽然 Atiyah 爵士对自己证明过程十分有把握,其论文也已向相关期刊投稿,但是从会前到会后,学者一直对此次证明过程存疑。
而在李忠的证明过程中,Reich 度量是证明中最重要的部分。Reich 度量不仅仅是李忠最近研究的新内容,同时也是证明黎曼猜想的重要工具。
但在会上,李忠教授并未对 Reich 度量及相关理论做过多声明。或许还需要等待李忠老师未来公开论文后才能一窥究竟。

李忠的证明过程也十分简洁,他的论文只有 2 页纸,而核心证明步骤只有一行。但这需要先对 Reich 度量进行了解,才能通过 Reich 度量对黎曼猜想进行证明。

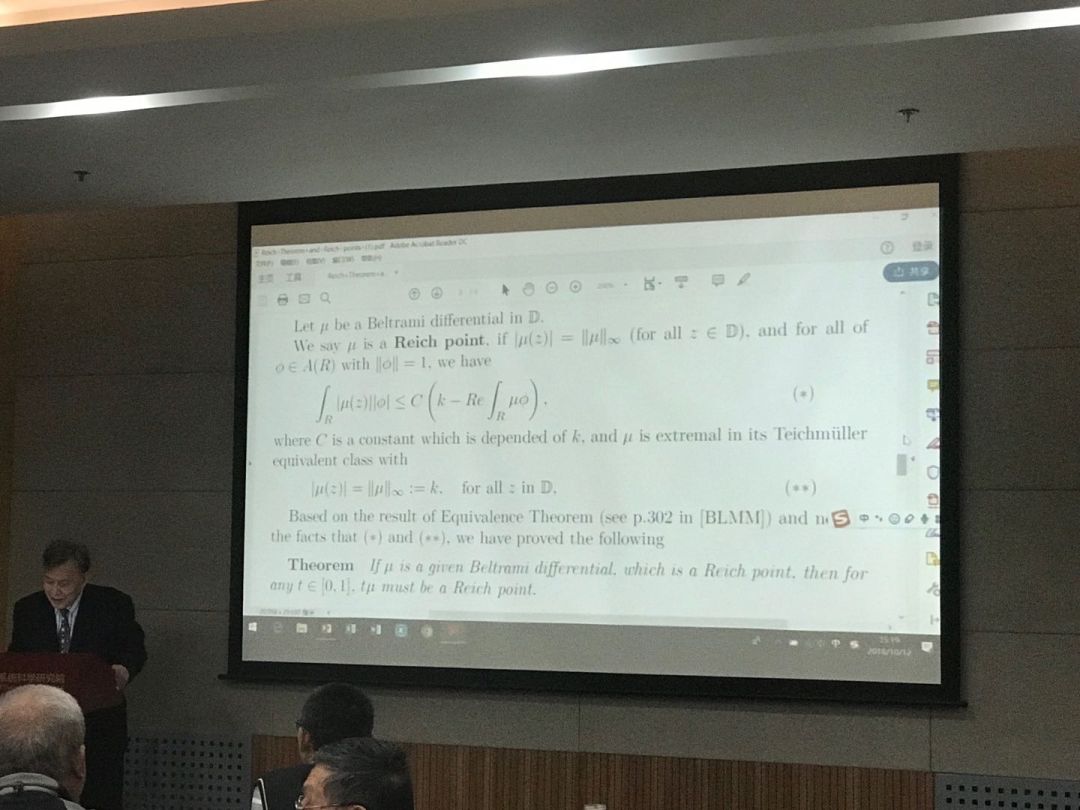
李忠教授指出,在 9 月 24 日的海德堡获奖者论坛中,Atiyah 对黎曼猜想的证明是物理学中精细结构常数 α 的副产品,这建立在冯·诺依曼和弗里德里希·希策布鲁赫工作的基础之上。
其中一个非常关键的问题就在于,这里的有界性没有得到证明。Atiyah 爵士证明中使用了物理意义下的有界量,而此次证明黎曼猜想本身就涉及到证明黎曼 zeta 函数是有界的,因此其证明过程并不完整。但使用 Reich 度量后,则可以明确证明黎曼 zeta 函数的有界性。同时,李忠教授认为,他的证明和自己的证明是可以相互印证的:Atiyah 爵士的思路并没有错,但仍需要更改度量。如果将度量改成 Reich 度量,Atiyah 爵士也是可以证明黎曼猜想的。

李忠在讨论会上十分谦虚地说,自己的工作是对 Atiyah 爵士工作的补充。他还透露,其实在海德堡论坛前,曾在清华大学进行过 Reich 度量的相关讨论。虽然当时李忠并未点透其与黎曼猜想证明的关系,但在场一些学者却已发现,这与黎曼猜想证明有着千丝万缕的联系。
目前来看。此次的报告会已经得到了多位数学界的大咖的认可。
数学家、北京大学数学科学学院教授郑忠国表示黎曼猜想已被证明。
郑教授写道:李忠利用Riech度量严格证明了黎曼假设。他的证明与数学家Atiyah(阿蒂亚老爵爷,此前曾做过黎曼猜想证明的报告)证明的关系可以简述如下:两人的思路相同,但Atiyah用一个量不合适,严格意义上证明是不完全的。李忠利用Riech度量以后证明就严格了。
数学家,北京大学数学科学学院原副院长,原中国数学会秘书长彭立中老师评评价说(此评论后由李忠教授转发给北大离退休老师群):
定义Riech度量(李-度量),证明Atiyah常数在该度量下是有限的数学常数,从而完成了RH之证明。李早于Atiyah证明了黎曼函数在李-度量下有界,从而RH成立。
按照惯例,报告之后不久,行业内会对李忠教授报告的手稿和论文进行评估,不久之后结果也会对外界公布,期待被载入数学史的一刻早点到来。
【李忠简介】
李忠,出生于1936年8月,现年82岁,系北京大学数学科学学院教授、博士生导师。他在1960年毕业于北京大学数学力学系,之后一直在北京大学任教,1987年-1991年担任北京大学数学系主任,曾任中国数学会常务理事兼秘书长及北京数学会理事长。他曾获国家教委科技进步奖一等奖,两次获得国家自然科学奖三等奖。被评为有突出贡献的中青年专家、国家优秀教师。他的主要研究领域为基础数学复分析,对拟共形映射与黎曼曲面的模空间理论有系统的研究,曾著有《复分析导引》、《拟共形映射及其在黎曼曲面论中的应用》等书。
【黎曼猜想】
“黎曼猜想” 是数学界迄今最重要的猜想之一,被克雷数学研究所列为 “有待解决的七大千禧问题”。而黎曼猜想为何如此难证,主要原因如下:
难点一:如果黎曼猜想(RH)被证否,并不会有特别严重的后果。
难点二:关于zeta函数,目前的结论集中在function equation,即modularity,即Langlands层面。但RH是一个更高层面的结论。
难点三:很难说出RH在模形式那边的对应物。
难点四:我们会证某些RH的类似物,但不知道怎么把结果转化到数域上。
90岁高龄的英国数学家阿蒂亚爵士于9月20日宣称证明出黎曼猜想,数学界为之一震。而9月24日,当阿蒂亚爵士仅用5页论文对其论证过后,外界反响并没有想象中的那般轰动。许多专家对他的证明结果选择缄默不言。而目前看来,外界普遍的观点还是不严整。
而就在此事余温尚存之际,同样是高龄的著名数学家,并且还是国人,就必然会引起一番热潮,尽管这份期待可能会非常谨慎。而更重要的是,这张网络疯传的报告预告中赫然写着“全新证明”、“所有步骤有严格详细解释与证明”,这些描述从读者角度看来,正是比阿蒂亚爵士更胜一筹。
与现年90岁的阿蒂亚爵士相似,李忠也是高龄学者。在公布要挑战证明黎曼猜想时,不乏有唱衰者。

事实上,对于学术,无论成败,探索精神都是前提。在探索真理的道路中,失败的经验并非毫无价值。若失败,也能让后来者在探索的道路上避开这些障碍。
自1859年黎曼猜想诞生以来,无数数学巨匠为之付出了心血。但这条破解之路上,虽然没人完全取得成功,但在这一过程中数学家们也为破解这一难题提供了很多思路与方法,例如:
1981年,荷兰三位数学家J.van de Lune、H.J.Riele te以及D.T.Winter用电子计算机来检验黎曼的假设,他们对最初的2亿个齐打函数的零点检验,证明黎曼的假设是对的;
1982年,前苏联数学家马帝叶雪维奇在前苏联杂志《Kibernetika》宣布,他利用电脑检验一个与黎曼猜想有关的数学问题,可以证明该问题是正确的,从而反过来可以支持黎曼的猜想很可能是正确的;
……
2018年,钮鹏程,西北工业大学应用数学系教授,讨论了Riemann zeta函数的非平凡零点的性质。
159年间,无数国内外数学家前赴后继地前去探索而后倒下,阿蒂亚爵士和李忠教授都不会是最后一位,还会有后来人。
编辑:顾军
责任编辑:樊丽萍
来源:DeepTech深科技、新智元





