
其实神奇的动物除了电影里有之外,科学界里也有许多,今天就来给大家说说科学界里的那些小动物!
影片《神奇的动物在哪里2》大受好评,除了震撼的电影特效外,里面的出现的小动物也是超级加分。
比如以澳大利亚针鼹为原型的嗅嗅。圆滚滚的身材配上亮晶晶的小眼睛,简直让人忍不住想抱着狂吸。

还有中国神兽驺吾,看似凶残的它其实内心也是住着一只小猫咪,要不然怎么会在遇到逗猫棒时变呆萌呢?

其实神奇的动物除了电影里有之外,科学界里也有许多。今天小编就来给大家说说科学界里的那些小动物!

凯库勒的衔尾蛇
19世纪,苯被发现,它的到来除了让化学家们感到兴奋之外也面临着一个难题—苯的结构式到底长啥样?
因为苯的分子中含有6个碳原子和6个氢原子,碳的化合价是四价,氢的化合价是一价,那么,1个碳原子就要和4个氢原子化合,6个碳原子该和12个氢原子化合,而苯怎么会是6个碳原于和6个氢原子化合。

来自德国的化学家凯库勒最终发现了苯环的结构式。
而他发现的方法也比较奇特了,因为他的灵感来源于一个梦。
他曾记载道:“我坐下来写我的教科书,但工作没有进展;我的思想开小差了。我把椅子转向炉火,打起瞌睡来了。
原子又在我眼前跳跃起来,这时较小的基团谦逊地退到后面。
我的思想因这类幻觉的不断出 现变得更敏锐了,现在能分辨出多种形状的大结构,也能分辨出有时紧密地靠近在一起的长行分子,它围绕、旋转,象蛇一样地动着。
看!那是什么?有一条蛇 咬住了自己的尾巴,这个形状虚幻地在我的眼前旋转着,象是电光一闪, 我醒了。我花了这一夜的剩余时间,作出了这个假想。”
跟被苹果砸中的牛顿一样,凯库勒通过衔尾蛇的灵感,首次满意地写出了苯的结构式,并且指出芳香族化合物的结构含有封闭的碳原子环。

苯环结构的诞生,也是有机化学发展史上的一块里程碑。
薛定谔的猫
1926年,奥地利物理学家薛定谔提出提出薛定谔方程,为量子力学奠定了坚实的基础。
他想出薛定谔猫思想实验,试图从宏观尺度阐述微观尺度的量子叠加原理的问题。
把一只喵喵放进了一个密封的盒子里,盒子里有一些放射性物质。这些放射性物质有50%的概率将会衰变并且放出毒气,来杀死这只猫;同时也有50%的概率放射性物质不会衰变,这样猫将活下来。
要想知道这只猫是否活着,我们得打开盒子才知道。

薛定谔的猫很好的描述了量子力学的真相:在量子系统中,一个原子或者光子可以同时以多种状态的组合形式存在,而这些不同的状态可能对应不同的甚至是矛盾的结果。
巴普洛夫的狗

1901年,俄罗斯生理学家巴甫洛夫在研究狗狗消化腺分泌时,发现了一个奇怪的现象:
狗狗看到食物或进食之前会出现流口水的现象,于是巴甫洛夫每次在喂食前都先发出一些信号(摇铃),连续了几次后,有一次他光摇铃而不喂食,发现狗狗依然会流口水。
然而,在重复训练之前,狗狗对于“铃声响”是不会有反应的。
巴甫洛夫得出的结论是:经过几次训练后,狗狗误以为“铃声等同于吃饭”,所以才会出现狗狗一听到“铃声”就流口水的现象,而这种现象就称为条件反射。
结合薛定谔的猫,小编不由得想起了一句话:生活机械得像巴普洛夫的狗,命运无奈得像薛定谔的猫。
洛伦茨的蝴蝶

美国气象学家罗伦兹在一次模拟气象图时,机算发现由于误差会以指数形式增长,在这种情况下,一个微小的误差随着不断推移造成了巨大的后果。
后来,他在一次演讲中提出了这一问题,并发表了著名的”蝴蝶效应“——亚马逊雨林一只蝴蝶翅膀偶尔震动,也许两周后就会引起美国德克萨斯州的一场龙卷风。
芝诺的乌龟
芝诺悖论是古希腊哲学家芝诺曾提出一系列关于运动的不可分性的哲学悖论。
一个人从A点走到B点,要先走完路程的1/2,再走完剩下总路程的1/2,再走完剩下的1/2,”如此循环下去,永远不能到终点。
当时芝诺为了让大家理解这个观点,还创造出物理学第一神兽芝诺的乌龟。
他让古希腊神话中善跑的英雄阿喀琉斯和乌龟一起赛跑。 在他和乌龟的竞赛中,他的速度为乌龟十倍,乌龟在前面100米跑,他在后面追,但他永远追上乌龟。
因为在竞赛中,追者首先必须到达被追者的出发点,所以当阿喀琉斯追到100米时,乌龟已经又向前爬了10米,于是,一个新的起点产生了;
阿喀琉斯必须继续追,而当他追到乌龟爬的这10米时,乌龟又已经向前爬了1米,阿喀琉斯只能再追向那个1米。
就这样,乌龟会制造出无穷个起点,它总能在起点与自己之间制造出一个距离,不管这个距离有多小,但只要乌龟不停地奋力向前爬,阿喀琉斯就永远也追不上乌龟!
也就是说,阿克琉斯永远也追不上乌龟!
这只龟的出现也困扰了数学家一千多年,不过最终微积分的出现合理的解决了这个问题。
斐波那契的兔子
意大利数学家斐波那契(Fi-bonacci , L.)在他的名著《算法之书》中提出的一个问题:
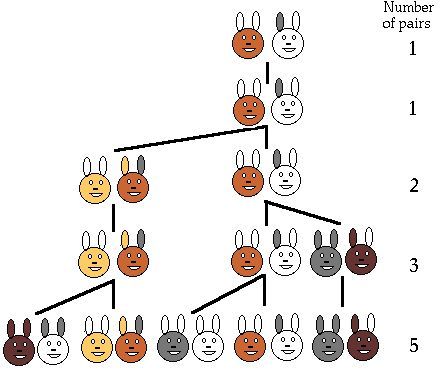
以兔子为例,兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。如果所有的兔子都不死,那么一年以后可以繁殖多少对兔子?
这个问题导致了著名的斐波那契数列:1,1,2,3,5,8,13,21,34,55,89,144,233(以递推的方法定义:F(1)=1,F(2)=1, F(3)=2,F(n)=F(n-1)+F(n-2)(n>=4,n∈N*))。
它是一个线性递归数列,因为是以兔子繁殖为例,它也叫兔子数列。
摩尔根的果蝇
美国生物学家与遗传学家摩尔根摩尔根虽然熟悉孟德尔动律,但从一开始就很怀疑这些理论。因为他认为这些定律可能只适合于豌豆。
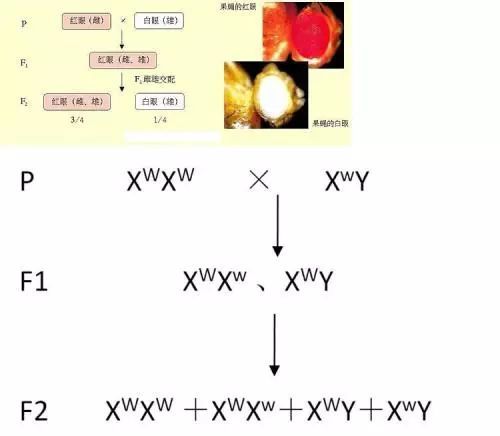
因为果蝇饲养容易,繁殖力强,体内染色体又简单(只有4对8条)。于是摩尔根利用果蝇进行遗传学研究。
最终发现了染色体是基因的载体,确立了伴性遗传规律。并发现位于同一染色体上的基因之间的连锁、交换和不分开等现象,建立了遗传学的第三定律——连锁交换定律。
其实科学家们拥有动物的还不止这些。比如斯金纳的鸽子、桑代克的猫、科勒的猩猩、托尔曼的老鼠、布里当的驴、童第周的鲫鱼、坎德尔的海兔、和奥斯内尔马什的蛇颈龙等。
编辑:朱颖婕 谢婉吟(实习)
责任编辑:樊丽萍
来源:公众号“超级数学建模”





